Question

Calculate the speed of the ball, vo in m/s, just after the launch. A bowling ball of mass m = 1.5 kg is launched from a spring compressed by a distance d = 0.21 m at an angle of θ = 32° measured from the horizontal. It is observed that the ball reaches a maximum height of h = 4.4 m, measured from the initial position of the ball. Let the gravitational potential energy be zero at the initial height of the bowling ball.

Answer 1

`v_0=17.3m/s`

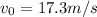
Step-by-step explanation:

In this problem we have three important moments; the instant in which the ball is released (1), the instant in which the ball starts to fly freely (2) and the instant in which has its maximum height (3). From the conservation of mechanical energy, the total energy in each moment has to be the same. In (1), it is only elastic potential energy; in (2) and (3) are both gravitational potential energy and kinetic energy. Writing this and substituting by known values, we obtain:

`E_1=E_2=E_3\\\\U_e_1=U_g_2+K_2=U_g_3+K_3\\\\(1)/(2)kd^2=mg(d\sin\theta)+(1)/(2)mv_0^2=mgh+(1)/(2)m(v_0\cos\theta)^2`

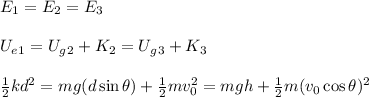
Since we only care about the velocity
`v_0`, we can keep only the second and third parts of the equation and solve:

`mgd\sin\theta+(1)/(2)mv_0^2=mgh+(1)/(2)mv_0^2\cos^2\theta\\\\(1)/(2)mv_0^2(1-\cos^2\theta)=mg(h-d\sin\theta)\\\\v_0=\sqrt{(2g(h-d\sin\theta))/(1-\cos^2\theta)}\\\\v_0=\sqrt{(2(9.8m/s^2)(4.4m-(0.21m)\sin32\°))/(1-\cos^232\°)}\\\\v_0=17.3m/s`

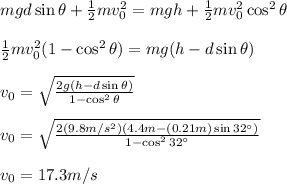
So, the speed of the ball just after the launch is 17.3m/s.