Question

The mayor of a town has proposed a plan for the construction of an adjoining community. A political study took a sample of 900 voters in the town and found that 62% of the residents favored construction. Using the data, a political strategist wants to test the claim that the percentage of residents who favor construction is above 59%. Find the value of the test statistic. Round your answer to two decimal places.

Answer 1

The value of the test statistics is 1.85.

Explanation:

We are given that a political study took a sample of 900 voters in the town and found that 62% of the residents favored construction.

Using the data, a political strategist wants to test the claim that the percentage of residents who favor construction is above 59%.

Let p = percentage of residents who favor construction.

SO, Null Hypothesis,
`H_0` : p
`\leq` 59% {means that the percentage of residents who favor construction is below or equal to 59%}

Alternate Hypothesis,
`H_A` : p > 59% {means that the percentage of residents who favor construction is above 59%}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
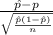`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
`\hat p` = percentage of residents who favor construction in a sample of 900 voters = 62%

n = sample of voters = 900

So, test statistics =
`\frac{0.62-0.59}{{\sqrt{(0.62(1-0.62))/(900) } } } }`

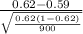
= 1.85

The value of the test statistics is 1.85.