Answer:
1.
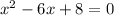
2.

3.
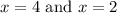
4.
Explanation:
1. When using substitution all we do would be is substituse the y for a 3.
This leaves us with the equation:
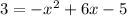
Rewriting it we get:
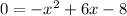
or if we shift the 0 to the other side:
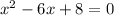
2. In order to factor the equation we can use the butterfly method:
![\left[\begin{array}{ccc}1&-4\\1&-2\end{array}\right]](https://img.qammunity.org/2023/formulas/mathematics/high-school/teskhcconnowaybh8a1x16asuj1s4uwu1s.png)
So it factors out to:

You can also use the quadratic formula.
3. To find the solutions we just set each factor to 0
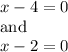
So the x-values would be:
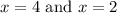
4. To find the solution to the system we just plug in the values and it turns out to be the same numbers as before.