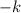Question

The magnetic field at the center of a wire loop of radius , which carries current , is 1 mT in the direction (arrows along the wire represent the direction of current). For the following wires, which all also carry current , indicate the magnitude (in mT) and direction of the magnetic field at the center (red point) of each configuration.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The magnetic field is
`B_(net) = (1)/(4) * mT`

And the direction is
`-\r k`

Step-by-step explanation:

From the question we are told that

The magnetic field at the center is
`B = 1mT`

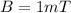
Generally magnetic field is mathematically represented as

`B = (\mu_o I)/(2R)`

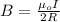
We are told that it is equal to 1mT

So

`B = (\mu_o I)/(2R) = 1mT`

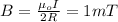
From the first diagram we see that the effect of the current flowing in the circular loop is (i.e the magnetic field generated)

`(\mu_o I)/(2R) = 1mT`

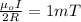
This implies that the effect of a current flowing in the smaller semi-circular loop is (i.e the magnetic field generated)

`B_1 = (1)/(2) (\mu_o I)/(2R)`

and for the larger semi-circular loop is

`B_2 = (1)/(2) (\mu_o I)/(2 * (2R))`

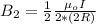
Now a closer look at the second diagram will show us that the current in the semi-circular loop are moving in the opposite direction

So the net magnetic field would be

`B_(net) = B_1 - B_2`

`= (1)/(2) (\mu_o I)/(2R) -(1)/(2) (\mu_o I)/(2 * (2R))`

`=(\mu_o I)/(4R) -(\mu_o I )/(8R)`

`=(\mu_o I)/(8R)`

`= (1)/(4) (\mu_o I)/(2R)`

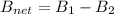
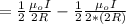
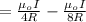
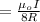
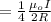
Recall
`(\mu_o I)/(2R) = 1mT`

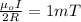
So

`B_(net) = (1)/(4) * mT`

Using the Right-hand rule we see that the direction is into the page which is
`-k`