Question

A glass lens, nglass=1.52, has a 127 nm thick antireflective film coating one side, nfilm=1.39. White light, moving through the air, is perpendicularly incident on the coated side of the lens. What is the largest wavelength of the reflected light that is totally removed by the coating? Assume that nair=1.00.

Answer 1

`\lambda = 706.12 nm`

Step-by-step explanation:

The optical path length for the reflection of light =
`2 n_(film) t`

For destructive interference,
`2 n_(film) t = (\lambda)/(2)`

The thickness of the anti-reflective film = 127 nm

The largest wavelength of the reflected light,
`\lambda = 4n_(film) t`

`\lambda = 4 * 1.39 *127 * 10^(-9)`

`\lambda = 706.12 * 10^(-9) m\\\lambda = 706.12 nm`

Answer 2

The wavelength is
`\lambda = 706nm`

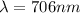
Step-by-step explanation:

From the question we are told that

The refractive index of the glass is
`n__(glass)} = 1.52`

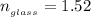
The thickness of film is
`D = 127nm = 127*10^(-9)m`

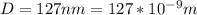
The refractive index of film
`n__(film)} = 1.39`

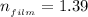
The refractive index of air is
`n__(air)} = 1.00`

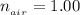
Generally the thickness of the film can be obtained mathematically from this expression

`D = (\lambda)/(4 * n__(film)) }`

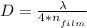
Where
`\lambda` is the wavelength

Making the wavelength the subject of the formula

`\lambda = 4 * n__(film)} * D`

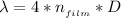
Substituting values

`\lambda = 4 *1.39 * 127 *10^(-9)`

`\lambda =7.06 *10^(-7)m = 706nm`