Answer:
0.1419 ( (if upper and lower cases are interchangeable)
0.348 ( if upper and lower cases are distinct letters)
Explanation:
Each digit has 36 possible choices as 26+10
computer generates six characters
there are only 26 choices for letters only, (if we assume upper and lower cases are interchangeable)
For number of letters-only arrangements =
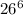 = 308915776
= 308915776
For number of alphanumeric arrangements =
 = 2176782336
= 2176782336
In order to find the probability of letters-only arrangements :
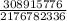
=>0.1419
Now, in different scenario if upper and lower cases are not interchangeable.
We will have 26+26+10=62 alphanumeric choices, and 52 alphabetic choices
Therefore, probability of letters-only arrangements will be
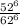
=>0.348