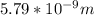Question

German physicist Werner Heisenberg related the uncertainty of an object's position ( Δ x ) to the uncertainty in its velocity ( Δ v ) Δ x ≥ h 4 π m Δ v where h is Planck's constant and m is the mass of the object. The mass of an electron is 9.11 × 10 − 31 kg. What is the uncertainty in the position of an electron moving at 2.00 × 10 6 m/s with an uncertainty of Δ v = 0.01 × 10 6 m/s ?

Answer 1

According to the information given, the Heisenberg uncertainty principle would be given by the relationship

`\Delta x \Delta v \geq (h)/(4\pi m)`

Here,

h = Planck's constant

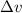`\Delta v` = Uncertainty in velocity of object

`\Delta x` = Uncertainty in position of object

m = Mass of object

Rearranging to find the position

`\Delta x \geq (h)/(4\pi m\Delta v)`

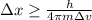
Replacing with our values we have,

`\Delta x \geq (6.625*10^(-34)m^2\cdot kg/s)/(4\pi (9.1*10^(-31)kg)(0.01*10^6m/s))`

`\Delta x \geq 5.79*10^(-9)m`

Therefore the uncertainty in position of electron is
`5.79*10^(-9)m`