Question

Statistics students at a community college wonder whether the cars belonging to students are, on average, older than the cars belonging to faculty. They select a random sample of 58 cars in the student parking lot and find the average age to be 8.5 years with a standard deviation of 6.2 years. A random sample of 41 cars in the faculty parking lot have an average age of 5.1 years with a standard deviation of 3.5 years. Note: The degrees of freedom for this problem is df = 93.033791. Round all results to 4 decimal places

Answer 1

There is evidence to support the claim that the cars belonging to students are, on average, older than the cars belonging to faculty.

Explanation:

We have to perform a hypothesis test on the difference between means.

The claim is that the cars belonging to students are, on average, older than the cars belonging to faculty.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2 > 0`

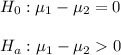
being μ1: population mean age of students cars, μ2: population mean age of faculty cars.

The significance level is assumed to be 0.05.

The information about the students cars sample is:

Mean M1: 8.5 years.

Standard deviation s1: 6.2 years.

Sample size n1: 58 cars.

The information about the faculty cars sample is:

Mean M2: 5.1 years.

Standard deviation s2: 3.5 years.

Sample size n2: 41 cars.

The difference between means is:

`M_d=M_1-M_2=8.5-5.1=3.4`

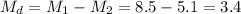
The standard error of the difference between means is:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)} =\sqrt{(6.2^2)/(58)+(3.5^2)/(58)}=√( 0.6628 +0.2988 )=√(0.9615)\\\\\\s_(M_d)=0.9806`

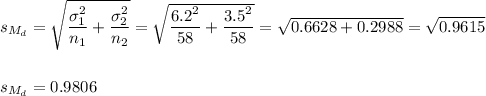
Now we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(3.4-0)/(0.9806)=3.4673`

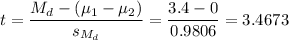
The degrees of freedom are 93.033791, so the P-value for this right tail test is:

`P-value=P(t>3.4673)=0.0004`

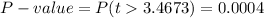
As the P-value is smaller than the significance level, the effect is significant and the null hypothesis is rejected.

There is evidence to support the claim that the cars belonging to students are, on average, older than the cars belonging to faculty.