Answer:
We can use the sample about 42 days.
Explanation:
Decay Equation:
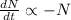
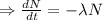
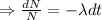
Integrating both sides
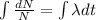
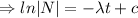
When t=0, N=
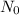 = initial amount
= initial amount
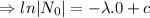
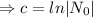
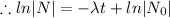
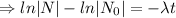
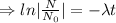 .......(1)
.......(1)
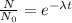 .........(2)
.........(2)
Logarithm:
130 days is the half-life of the given radioactive element.
For half life,
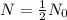 ,
,
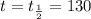 days.
days.
we plug all values in equation (1)
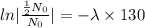
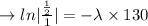
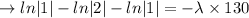
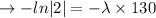
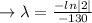
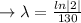
We need to find the time when the sample remains 80% of its original.
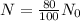
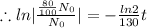
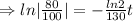
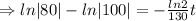
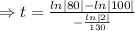
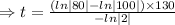
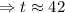
We can use the sample about 42 days.