Question

The time for this event for boys in secondary school is known to possess a normal distribution with a mean of 460 seconds and a standard deviation of 40 seconds. The fitness association wants to recognize the fastest 10% of the boys with certificates of recognition. What time would the boys need to beat in order to earn a certificate of recognition from the fitness association

Answer 1

The time that the boys need to beat in order to earn a certificate of recognition from the fitness association is 511.264 seconds.

Explanation:

We are given that the time for this event for boys in secondary school is known to possess a normal distribution with a mean of 460 seconds and a standard deviation of 40 seconds.

The fitness association wants to recognize the fastest 10% of the boys with certificates of recognition.

Let X = time for this event for boys in secondary school

SO, X ~ Normal(
`\mu=460,\sigma^(2) =40^(2)`)

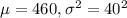The z-score probability distribution for normal distribution is given by;

Z =
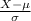`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean time = 460 seconds

`\sigma` = standard deviation = 40 seconds

The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.

Now, it is given that the fitness association wants to recognize the fastest 10% of the boys with certificates of recognition, which means;

P(X > x) = 0.10 {where x is the required time which boy need to beat}

P(
`(X-\mu)/(\sigma)` >
`(x-460)/(40)` ) = 0.10

P(Z >
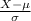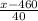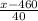`(x-460)/(40)` ) = 0.10

So, the critical value of x in the z table which represents the top 10% of the area is given as 1.2816, that is;

`(x-460)/(40) =1.2816`

`{x-460}{} =1.2816* 40`

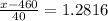
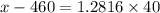
`x` = 460 + 51.264 = 511.264 seconds

Hence, the time that the boys need to beat in order to earn a certificate of recognition from the fitness association is 511.264 seconds.