Question

A certain circle can be represented by the following equation. x2 + y2 + 10x + 12y + 25 = 0. What is the center of this circle? What is the radius of this circle? Please help!

Answer 1

Let's try to complete the squares.

The x-part starts with
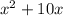`x^2+10x`, which is the beginning of
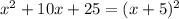`x^2+10x+25=(x+5)^2`. So, we'll think of
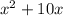`x^2+10x` as
`(x+5)^2-25`

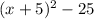
Similarly, we have that

`y^2+12y = (y+6)^2-36`

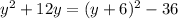
So, the equation becomes

`x^2 + y^2 + 10x + 12y + 25 = 0 \iff (x+5)^2-25 + (y+6)^2-36+25=0 \iff (x+5)^2+ (y+6)^2-36=0 \iff (x+5)^2+ (y+6)^2=36`

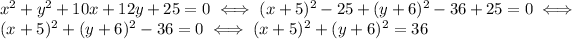
Now we have writte the equation of the circle in the form

`(x-k)^2+(y-h)^2=r^2`

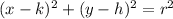
When the equation is in this form, everything is more simple: the center is
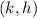`(k,h)` and the radius is
`r`.

Answer 2

Center// (-5,-6)

Radius// 6