Question

At a research facility that designs rocket engines, researchers know that some engines fail to ignite as a result of fuel system error. From a random sample of 40 engines of one design, 14 failed to ignite as a result of fuel system error. From a random sample of 30 engines of a second design, 9 failed to ignite as a result of fuel system error. The researchers want to estimate the difference in the proportion of engine failures for the two designs. Which of the following is the most appropriate method to create the estimate?

a. A one-sample z-interval for a sample proportion
b. A one-sample z-interval for a population proportion
c. A two-sample z-interval for a population proportion
d. A two-sample z-interval for a difference in sample proportions
e. A two-sample z-interval for a difference in population proportions

Answer 1

E

Explanation:

A two-sample z-interval for a difference in population proportions

Answer 2

d) A two-sample z-interval for a difference in sample proportions

Explanation:

Explanation:-

Given data a random sample of 40 engines of one design, 14 failed to ignite as a result of fuel system error.

First sample proportion
`p_(1) = (14)/(40) = 0.35`

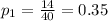
Given data random sample of 30 engines of a second design, 9 failed to ignite as a result of fuel system error.

second sample proportion
`p_(2) = (9)/(30) = 0.30`

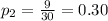
Null hypothesis: H₀: Assume that there is no significant between the two designs

H₀: p₁ = p₂

Alternative Hypothesis: H₁:

H₁: p₁ ≠ p₂

The test statistic

`Z = \frac{p_(1)-p_(2) }{\sqrt{p q((1)/(n_(1) ) + (1)/(n_(2) ) } )}`

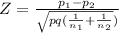
where
`p = (n_(1) p_(1)+n_(2) p_(2) )/(n_(1) +n_(2) )`

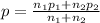
q =1-p