Question

Two long, parallel wires are attracted to each other by a force per unit length of 305 µN/m. One wire carries a current of 25.0 A to the right and is located along the line y = 0.470 m. The second wire lies along the x axis. Determine the value of y for the line in the plane of the two wires along which the total magnetic field is zero.

Answer 1

To solve this problem we will use the concepts related to the electromagnetic force related to the bases founded by Coulumb, the mathematical expression is the following as a function of force per unit area:

`(F)/(L) = (kl_1l_2)/(d)`

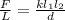
Here,

F = Force

L = Length

k = Coulomb constant

I =Each current

d = Distance

Force of the wire one which is located along the line y to 0.47m is
`305*10^(-6)N/m` then we have

`l_2 = (F)/(L) ((d)/(kl_1))`

`l_2 = (305*10^(-6)N/m)((0.470m)/((2*10^(-7))(25A))))`

`l_2 = 28.67A`

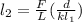
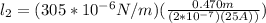
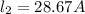
Considering the B is zero at

`y = y_1`

`(kI_2)/(2\pi y) =(kI_1)/(2\pi y_1)`

`((4\pi*10^(-7))(28.67))/(2\pi (y_1)) = ((4\pi *10^(-7))(25))/(2\pi (0.47-y_1))`

`y_1 = 0.25m`

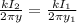
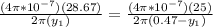
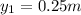
Therefore the value of y for the line in the plane of the two wires along which the total B is zero is 0.25m