Question

Find the vertical asymptote(s).

Answer 1

Answer: x = 1

By "doing the math" from the function given:

Given:

`f (x) =\displaystyle ((x+1)(x-7)(x-10))/((x-1)(x-7)(x-10))`

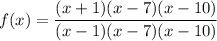
Terms in both the numerator and denominator are equal to 1:

`f (x) =\displaystyle ((x+1))/((x-1))`

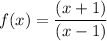
We cannot have a denominator equal to 0, because you cannot divide by 0, so the vertical asymptote is x = 1 since 1 - 1 = 0. This can also be found by setting the denominator equal to 0 and solving for x.

By graphing:

A vertical asymptote, put simply, is a vertical line "within" the domain, but not a part of the graph. I will graph the equation given and see what we come up with.

-> See attached

Either way, the answer to your problem is:

x = 1

Answer 2

x = 1

Explanation:

To find the vertical asymptote(s) we set the denominator to 0, but first we have to factor and simplify the function

`f(x)=((x+1)(x-7)(x+10))/((x-1)(x-7)(x+10))`

step 1 the function is already factored so we just have to simplify it by canceling like terms

`f(x)=(x+1)/(x-1)`

step 2 set denominator to 0 and solve for x

x - 1 = 0

step 3 add 1 to both sides

x = 1