Answer:
Probability that at least 40 students have purchased textbooks from an off-campus vendor at least once during their college career is 0.0688.
Explanation:
We are given that a survey of students at a large university found that 82% had purchased textbooks from an off-campus vendor at least once during their college career.
Also, 45 students are randomly sampled.
Let
 = sample proportion of students who have purchased textbooks from an off-campus vendor at least once during their college career.
= sample proportion of students who have purchased textbooks from an off-campus vendor at least once during their college career.
The z-score probability distribution for sample proportion is given by;
Z =
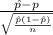 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion =
= sample proportion =
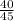 = 0.89
= 0.89
p = population proportion of students who had purchased textbooks from an off-campus vendor at least once during their college career = 82%
n = sample of students = 45
Now, probability that at least 40 students have purchased textbooks from an off-campus vendor at least once during their college career is given by = P(

 0.89)
0.89)
P(

 0.89) = P(
0.89) = P(
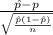

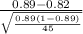 ) = P(Z
) = P(Z
 1.50) = 1 - P(Z < 1.50)
1.50) = 1 - P(Z < 1.50)
= 1 - 0.9332 = 0.0688
The above probability is calculate by looking at the value of x = 1.50 in the z table which ha an area of 0.9332.
Therefore, the required probability is 0.0688.