Answer:
Step-by-step explanation:
a) the period of the motion:
In order to calculate, we have the following formula.
f = 1/T whereas, T = 1/f. So, we need frequency first to calculate period of the motion.
In the question, we have been given amplitude and maximum acceleration. So, we can use the formula of maximum acceleration to calculate the frequency. Here's how:
Maximum acceleration = (2πf)² x A
where, A is amplitude.
a(max) = maximum acceleration
By rearranging the equation and making the frequency our subject and plugging in the values of given quantities then we have:
f = 138.80 hertz
Now, we can calculate, period of the motion by plugging in the value of frequency in the equation of period mentioned above.
Period of the motion = T = 1/f
T= 1/138.80
T = 7.204 x
 seconds.
seconds.
b) Maximum Speed of the particle
In order to calculate max. speed of the particle, we have to use following formula:
Max. Speed = 2πf x A
Max. Speed = ( 2 x 3.14 x 138.80 x 7.1x
 )
)
Max. Speed = 6.19 m/s
c) Total mechanical energy of the oscillator
Total mechanical energy of the oscillator is the sum of kinetic energy and potential energy and for which we have formula to calculate total mechanical energy of the oscillator:
Total Mechanical Energy = T.E = K.E + P.E
T.E = 2m
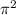
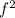

we do have values of all the quantities and now by just plugging in the values we will get the total mechanical energy of the oscillator.
T.E = 2 x 0.047 x
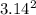 x
x
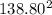 x
x
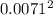
T.E = 0.90 J
d) Magnitude of the force on the particle when the particle is at its maximum displacement.
F = -KA here, amplitude is used because it is the maximum displacement from the mean position.
where K = -m ω² x A
ω = 2πf = 2 x 3.14 x 138.80
ω = 871.66
F = -(0.047 x 871.66² x 0.0071²)
F = - 1.8 N
e) when the displacement is at half
F = -Kx A/2
A/2 = 0.0071 / 2
A/2 = 0.0035
F = - m ω² x A/2
F = - (0.047 x 871.66² x 0.0035)
F = - 125 N