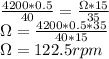Question

y ????, the air viscosity µ, the wind velocity V, the rotation rate Ωand the number of blades n. (a) Write this relationship in dimensionless form. A model windmill, of diameter 50 cm, develops 3.8 kW at sea level when V  40 m/s and when rotating at 4200 rpm. (b) What power will be developed by a geometrically and dynamically similar prototype, of diameter 15 m, in winds of 35 m/s at 500 m standard altitude from sea level? (c) What is the appropriate rotation rate of the prototype?

Answer 1

a)
`(P)/(\rho v^(3)D^(2) ) = f((\Omega D)/(v), n)`

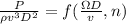
b) P = 2184.57 kW

c)
`\Omega = 122.5 rpm`

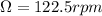
Step-by-step explanation:

Pressure = P

Density =
`\rho`

Diameter = D

Velocity = v

Rate of rotation = Ω

number of blades = n

a) The relationship for the model is given by:

`(P)/(\rho v^(3)D^(2) ) = f((\Omega D)/(v), n)`

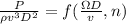
b) The Power developed geometrically and dynamically similar prototype:

The data corresponding to the model:

`P_(mod) = 3.8 kW\\v_(mod) = 40 m/s\\D_(mod) = 50 cm = 0.5 m\\\rho_(mod) = 1.2255 kg/m^(3)\\ \Omega = 4200 rpm`

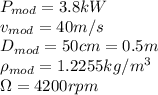
The data corresponding to the prototype

`P_(prot) = ? \\v_(prot) = 35 m/s\\D_(prot) = 15 m\\\rho_(prot) = 1.1685 kg/m^(3)`

`((P)/(\rho v^(3)D^(2) ) )_(mod) = ((P)/(\rho v^(3)D^(2) ) )_(prot)`

`(3.8)/(1.2255 * 40^(3) * 0.5^(2) )= (P)/(1.1685 * 35^(3) * 15^(2) )\\P = (3.8 * 1.1685 * 35^(3) * 15^(2))/(1.2255 * 40^(3) * 0.5^(2) )`

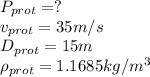
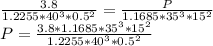
P = 2184.57 kW

c) To calculate the appropriate rotation rate for the prototype

`((\Omega D)/(v))_(model) = ((\Omega D)/(v))_(prot)`

`(4200*0.5)/(40)= (\Omega * 15)/(35)\\\Omega = (4200*0.5*35)/(40*15)\\\Omega = 122.5 rpm`