Answer:
a) E = k Ze (1- r³ / R³) 1/r², b) E=0, c) E = -6.62 10¹⁰ N / C
Step-by-step explanation:
a) For this we can use the law of Gauus
Ф = E- dA =
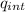 / ε₀
/ ε₀
where we take a sphere as a Gaussian surface, so that the electric field lines and the radii of the sphere are parallel, consequently the dot product is reduced to the algebraic product
E A =q_{int} / ε₀
the area of a sphere
A = 4π r²
E 4π r² = q_{int} / ε₀
E = 1 / 4πε₀ q_{int} / r²
k = 1 /4π ε₀
E = k q_{int} / r² (1)
let's analyze the charge inside the gaussian sphere,
let's use the concept of density for electrons, since they indicate that the charge is evenly distributed
ρ = Q / V
where the volume of the sphere is
V = 4/3 πr³
Qe = ρ V
Qe = ρ 4 / 3π r³
the density of the electrons is
ρ = Ze 3 / (4π R³)
where R is the atomic radius
we substitute
Qe = Ze r³/ R³
for protons they are in a very small space, the atomic nucleus, so we can superno that they are a point charge.
The net charge inside our Gaussian surface, the charge of the protoens plus the charge of the electroens (Qe)
q_{int} = q_proton + Q_electron
q_{int} = + Ze - Qe
q_{int} = + Ze - Ze r³ / R³
q_{int} = Ze (1- r³ / R³)
we substitute in equation 1
E = k Ze (1- r³ / R³) 1/r²
b) on the surface of the atom r = R
therefore the electric field is zero
E = 0
c) Calculate the electric field for the Uranium for
r = R / 2 = 0.10 10⁻⁹ / 2 = 0.05 10⁻⁹ = 5 10⁻¹¹ m
E = 8.99 10⁹ 92 1.6 10⁻¹⁹ (1-1/2)³ 1/ (5 10⁻¹¹)²
E = -6.62 10¹⁰ N / C