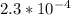Question

An aluminum cylinder with a radius of 2.5 cmcm and a height of 82 cmcm is used as one leg of a workbench. The workbench pushes down on the cylinder with a force of 3.2×104N3.2×104N. What is the compressive strain of the cylinder? Young's modulus for aluminum is 7.0×1010Pa7.0×1010Pa. Express your answer using two significant figures.

Answer 1

To solve the problem, it will be necessary to apply the concepts related to Young's Modulus, which defines the relationship between stress and strain in a body. This mathematical relationship is explained below

`\text{Young Modulus} = \frac{\text{Stress}}{\text{Strain}}`

`\upsilon = (\sigma)/(\epsilon)`

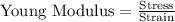
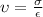
But here,

`\sigma = (F)/(A) = (F)/(\pi r^2)`

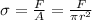
Where,

A = Area

F = Force

r = Radius

In the formula of Young modulus we have then,

`\upsilon= ((F)/(A))/(\epsilon)`

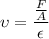
Replacing,

`7.0*10^(10) = ((3.2*10^4)/(\pi (2.5*10^(-2))^2))/(\epsilon)`

`\epsilon = ((3.2*10^4)/(\pi (2.5*10^(-2))^2))/(7.0*10^(10))`

`\epsilon = 2.3*10^(-4)`

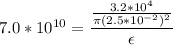
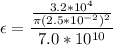
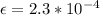
Therefore the strain is
`2.3*10^(-4)`