Question

A researcher wants to test if the mean price of houses in an area is greater than $145,000. Suppose we make the test at the 2% significance level. A sample of 36 houses selected from this area produces a mean price of $149,750 and a standard deviation of $24,600. What is the value of the test statistic?

Answer 1

The value of the test statistic is 1.158.

Explanation:

We are given that a researcher wants to test if the mean price of houses in an area is greater than $145,000.

A sample of 36 houses selected from this area produces a mean price of $149,750 and a standard deviation of $24,600.

Let
`\mu` = mean price of houses in an area.

SO, Null Hypothesis,
`H_0` :
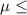`\mu \leq` $145,000 {means that the mean price of houses in an area is smaller than or equal to $145,000}

Alternate Hypothesis,
`H_A` :
`\mu` > $145,000 {means that the mean price of houses in an area is greater than $145,000}

The test statistics that will be used here is One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

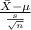where,
`\bar X` = sample mean price of houses selected = $149,750

s = sample standard deviation = $24,600

n = sample of houses = 36

So, test statistics =
`(149,750-145,000)/((24,600)/(√(36) ) )` ~
`t_3_5`

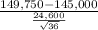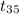
= 1.158

The value of the test statistic is 1.158.