Question

Twenty-five blood samples were selected by taking every seventh blood sample from racks holding 187 blood samples from the morning draw at a medical center. The white blood count (WBC) was measured using a Coulter Counter Model S. The mean WBC was 8.636 with a standard deviation of 3.9265.

(a) Construct a 95 percent confidence interval for the true mean using the FPCF.

(b) What sample size would be needed for an error of +/- 1.5 with 95 percent confidence?

Answer 1

a) The 95% confidence interval for the true mean is:

`8.0695\leq \mu\leq9.2025`

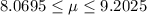
b) This margin of error can be achieved with a sample of size 27 individuals.

Explanation:

a) We have to construct a 95% confidence interval for the populations mean WBC.

The sample results, from a sample size n=187, are:

• Sample mean: 8.636
• Standard deviation: 3.9265

As we are using the sample standard deviation to estimate the population standard deviation, we will use the t-statistic.

The degrees of freedom are:

`df=n-1=187-1=186`

The t-statistic for a 95% interval and 186 degrees of freedom is t=1.9728.

Now, we can calculate the margin of error of the confidence interval:

`E=t \cdot s/√(n)=1.9728*3.9265/√(187)=7.7462/13.6748=0.5665`

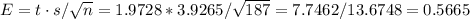
The upper and lower bound of the confidence interval are:

`LL=\bar x-t \cdot s/√(n)=8.636-0.5665=8.0695\\\\UL=\bar x+t \cdot s/√(n)=8.636+0.5665=9.2025`

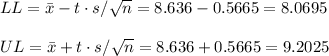
The 95% confidence interval for the true mean is:

`8.0695\leq \mu\leq9.2025`

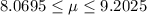
b) As the confidence level is equal, the t-value is the same.

But the sample size has to be adjusted to have an margin of error of +/-1.5.

We use the formula for the margin of error:

`E=t \cdot s/√(n)=1.9728*3.9265/√(n)=7.7462/√(n)=1.5\\\\\\n=((7.7462)/(1.5))^2=5.1641^2=26.67\approx27`

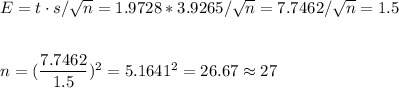
This margin of error can be achieved with a sample of size 27 individuals.