Answer:
0.00636 ft/min
Explanation:
considering 'r' as radius of base at time t
'h' as height at time t
V = volume of cone at time t
Given: dV/dt = 10 ft³/min
Find: dh/dt when h = 17 ft
As we know that equation of volume is defined as
V = (1/3)πr²h
[The diameter of the base of the cone is approximately three times the altitude.therefore, 2r = 3h, r = (3/2)h ]
V = (1/3)π[(3/2)h]2h
= (3/4)πh³
= ()πh²()
13 = () π (17)²(dh/dt)
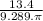 =
=

 =
=
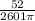
 = 0.00636 ft/min
= 0.00636 ft/min
therefore, the pile is changing at the rate of 0.00636 ft/min