Question

Let A and B represent two variants (alleles) of the DNA at a certain locus on the genome. Assume that 40% of all the alleles in a certain population are type A and 30% are type B. The locus is said to be in Hardy-Weinberg equilibrium if the proportion of organisms that are of type AB is (0.40)(0.30) = 0.12. In a sample of 300 organisms, 44 are of type AB. Can you conclude that this locus is not in Hardy-Weinberg equilibrium? Find the P-value and state a conclusion. Round the answer to four decimal places.

Answer 1

P-value=0.1778.

The null hypothesis is not rejected.

There is not enough evidence to support the claim that the population is not in Hardy-Weinberg equilibrium.

Explanation:

We have to perform a hypothesis testing on the actual population proportion.

The claim is that the population is not in Hardy-Weinberg equilibrium. That is that the proportion of organisms that are type AB is not 0.12.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.12\\\\H_a:\pi\\eq0.12`

The significance level is assumed to be 0.05.

The sample size is 300.

The sample proportion is p=0.147

`p=44/300=0.147`

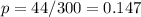
The standard deviation is:

`\sigma_p=\sqrt{(p(1-p))/(N)}=\sqrt{(0.12*0.88)/(300)}=√(0.000352)=0.0188`

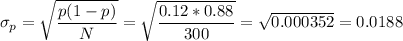
Now, we can calculate the z-statistic as:

`z=(p-\pi-0.5/n)/(\sigma_p)=(0.147-0.12-0.5/300)/(0.0188)=(0.0253)/(0.0188)= 1.3475`

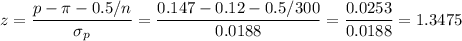
The P-value for a two-tailed test is:

`P-value=2*P(z>1.3475)=0.1778`

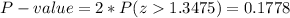
The P-value is bigger than the significant level, so the effect is not significant and the null hypothesis is not rejected.

There is not enough evidence to support the claim that the population is not in Hardy-Weinberg equilibrium.