Answer:
$398.48
Step-by-step explanation:
For calculating the saving amount, first need to calculate the economic order quantity, total cost etc
The economic order quantity is

where,
Annual demand is
= 790 packaging crates × 12 months
= 9,480 crates
And, the carrying cost is
= $10 × 39%
= $3.90
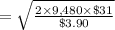
= 388 units
Now the total cost is
= Annual ordering cost + Annual carrying cost
= Annual demand ÷ Economic order quantity × ordering cost per order + Economic order quantity ÷ 2 × carrying cost per unit
= 9,480 ÷ 388 × $31 + 388 ÷ 2 × $3.90
= $757.42 + $756.60
= $1,514.02
Now the total cost in case of 790 packing crates is
= Annual ordering cost + Annual carrying cost
= Annual demand ÷ Economic order quantity × ordering cost per order + Economic order quantity ÷ 2 × carrying cost per unit
= 9,480 ÷ 790 × $31 + 790 ÷ 2 × $3.90
= $372 + $1,540.50
= $1,912.50
Therefore, the annual saving cost is
= $1,912.50 - $1,514.02
= $398.48