Question

A right triangle whose hypotenuse is 3 centimeters long is revolved about one of its legs to generate a right circular cone. Find the radius, height, and volume of the right cone that will have the greatest volume when constructed this way.

Answer 1

The height of the right circular cone when constructed this way is
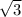`\sqrt3` cm.

The radius of the right circular cone when constructed this way is
`\sqrt6` cm.

The volume of the right circular cone when constructed this way is
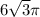`6\sqrt3 \pi` cm³.

Explanation:

Given that,

A right triangle whose hypotenuse is 3 cm long is revolved .

Then other two legs of the triangle will be radius and height of the cone.

Assume the height and radius of the cone be h and r respectively.

From Pythagorean Theorem :

h²+r²=3²

⇒ r²= 9 - h²

Then the volume of the cone is

V= π r²h

⇒ V= π(9-h²)h [ ∵ r²= 9 - h²]

⇒V= π(9h - h³)

Differentiating with respect to h

V'=π(9 - 3h²)

Again differentiating with respect to h

V''= π(-6h)

⇒V''= (-6πh)

To maximum or minimum ,we set V'=0

π(9 - 3h²)=0

⇒3h²=9

⇒h²=3

`\Rightarrow h=\sqrt3`

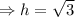
Now,
`V''|_(h=\sqrt3)=-6\pi (\sqrt3)<0`.

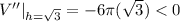Since at
`h=\sqrt3`,V''<0.

The volume of cone is maximum at
`h=\sqrt3` cm when constructed this way.

The height of the right circular cone when constructed this way is
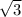`\sqrt3` cm.

The radius of the right circular cone when constructed this way
`r=\sqrt{9-(\sqrt3)^2`

=
`√(9-3)`

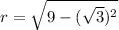
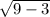
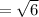`=\sqrt6` cm.

The volume of the right circular cone when constructed this way is

=π r²h

`=\pi (\sqrt6)^2\sqrt3`

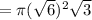
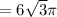`=6\sqrt3 \pi` cm³