Question

Let E(r) represent the electric field due to the charged ball throughout all of space. Which of the following statements about the electric field are true? Check all that apply. View Available Hint(s) Check all that apply. E(0)=0. E(rb)=0. limr→[infinity]E(r)=0. The maximum electric field occurs when r=0. The maximum electric field occurs when r=rb. The maximum electric field occurs as r→[infinity].

Answer 1

Correct -> E(0) = 0

Correct ->
`\lim_(r \to \infty) E(r) = 0`

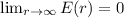
Correct -> The maximum electric field occurs when r = rb.

Step-by-step explanation:

The electric field formula due to a particle in space is

`\vec{E} = (1)/(4\pi \epsilon_0)(q)/(r^2)\^(r)`

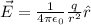
However, inside the ball the electric field is different.

Applying Gauss' Law inside the ball gives:

`\int {\vec{E}} \, da = (Q_(\rm enc))/(\epsilon_0)\\ E4\pi r^2 = (qr^3)/((rb)^3\epsilon_0)\\E = (1)/(4\pi\epsilon_0)(r)/((rb)^3)`

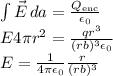
- At r = 0, the above formula yields 0 as well. Therefore the statement E(0) = 0 is correct.

- Due to the above formula,

`E(rb) = (1)/(4\pi \epsilon_0)(q(rb))/((rb)^3) = (1)/(4\pi\epsilon_0)(q)/((rb)^2) \\eq 0`

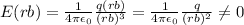
Therefore, the statement "E(rb) = 0" is wrong.

-
`\lim_(r \to \infty) E(r) = 0`

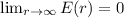
This statement is correct. Since r is in the denominator, 1/∞ can be taken zero.

- The maximum electric field does not occur at r = 0.

- If 'rb' is the radius of the ball, then the maximum electric field occurs when r = rb.

- At infinity, the electric field goes to zero, therefore the maximum electric field does not occur as r -> infinity.