Question

What is the equation, in point-slope form, of the line that is parallel to the given line and passes through the point (4, 1)?

y − 1 = −2(x − 4)
y – 1 = Negative one-half(x – 4)
y – 1 = One-half(x – 4)
y − 1 = 2(x − 4)

Answer 1

To find the equation in point-slope form of a line parallel to the given line and passing through a point, we use the fact that parallel lines have the same slope.

Step-by-step explanation:

To find the equation in point-slope form of a line parallel to the given line and passing through the point (4, 1), we need to use the fact that parallel lines have the same slope.

The given line has an equation in point-slope form as y - 1 = -2(x - 4). The slope of this line, which is -2, will be the slope of the parallel line we are looking for.

Using the point-slope form equation y - y1 = m(x - x1), and substituting the values y1 = 1, x1 = 4, and m = -2, we can write the equation as y - 1 = -2(x - 4).

Answer 2

Given:

The line parallel to the given line containing the points (-3,3) and (-2,1).

Also, the parallel line passes through the point (4,1).

We need to determine the equation of the line in slope - intercept form.

Slope:

Since, the two lines are parallel, then their slopes are equal.

Thus, the slope of the parallel line can be determined using the formula,

`m=(y_2-y_1)/(x_2-x_1)`

Substituting the points (-3,3) and (-2,1), we get;

`m=(1-3)/(-2+3)`

`m=(-2)/(1)`

`m=-2`

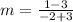
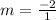
Thus, the slope of the line is
`m=-2`

Equation of the line:

The equation of the line can be determined using the formula,

`y-y_1=m(x-x_1)`

Since, the line passes through the point (4,1), let us substitute the point (4,1) in the above formula, we have;

`y-1=-2(x-4)`

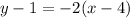
Thus, the equation of the line is
`y-1=-2(x-4)`

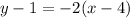
Hence, Option a is the correct answer.