Question

Suppose oil spills from a ruptured tanker and spreads in a circular pattern. If the radius of the oil spill increases at a constant rate of 1.5 m/s, how fast is the area of the spill increasing when the radius is 30 m?

Answer 1

The area of the oil spill is increasing at a rate 180 π m²/s, when the radius is 30 m.

Explanation:

Derivative Rule:

• 
  `(d)/(dx)x^n=nx^(n-1)`
• 
  `(d)/(dx)(y^n)=ny^(n-1)(dy)/(dx)`

Given that

The radius of the oil spill increases at a rate 1.5 m/s.

i.e
`(dr)/(dt)= 1.5\ m/s`

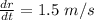
We need to find the rate of area increase i.e
`(dA)/(dt)` .

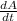We know,

The area of the oil spills A =
`\pi r^2` ( since it spreads in circular pattern)

`\therefore A=\pi r^2`

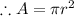
Differentiating with respect to t

`(dA)/(dt)=\pi. 2r(dr)/(dt)`

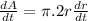
Plug the value of
`(dr)/(dt) =1.5 \ m/s`

`(dA)/(dt)=\pi. 2r(3\ m/s)`

`\Rightarrow (dA)/(dt)=6\pi r \ m/s`

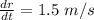
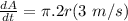
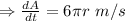
Plug r= 30 m

`\Rightarrow (dA)/(dt)=6\pi (30\ m) \ m/s`

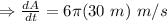
=180 π m²/s

The area of the oil spill is increasing at a rate 180 π m²/s, when the radius is 30 m.