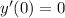Question

A mass weighing 4 lb stretches a spring 2 in. Suppose that the mass is given an additional 6-in displacement in the positive direction and then released. The mass is in a medium that exerts a viscous resistance of 6 lb when the mass has a velocity of 3 ft/s. Under the assumptions discussed in this section, formulate the initial value problem that governs the motion of the mass.

Answer 1

`(1)/(8) y'' + 2y' + 24y=0`

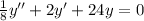
Step-by-step explanation:

The standard form of the 2nd order differential equation governing the motion of mass-spring system is given by

`my'' + \zeta y' + ky=0`

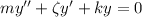
Where m is the mass, ζ is the damping constant, and k is the spring constant.

The spring constant k can be found by

`w - kL=0`

`mg - kL=0`

`4 - k(1)/(6)=0`

`k = 4* 6 =24`

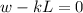
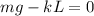
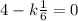
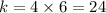
The damping constant can be found by

`F = -\zeta y'`

`6 = 3\zeta`

`\zeta = (6)/(3) = 2`

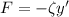
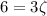
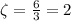
Finally, the mass m can be found by

`w = 4`

`mg=4`

`m = (4)/(g)`

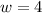
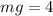
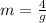
Where g is approximately 32 ft/s²

`m = (4)/(32) = (1)/(8)`

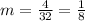
Therefore, the required differential equation is

`my'' + \zeta y' + ky=0`

`(1)/(8) y'' + 2y' + 24y=0`

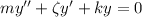
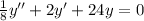
The initial position is

`y(0) = (1)/(2)`

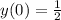
The initial velocity is

`y'(0) = 0`