Question

"The International Space Station (ISS) orbits at a distance of 350 km above the surface of the Earth. (a) Determine the gravitational field strength that astronauts onboard the ISS would experience. (b) Calculate the orbital velocity of the ISS. (c) Determine the period of the ISS orbit around Earth"

Answer 1

(a) g = 8.82158145
`m/s^2`.

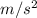(b) 7699.990192m/s.

(c)5484.3301s = 1.5234 hours.(extremely fast).

Step-by-step explanation:

(a) Strength of gravitational field 'g' by definition is

`g = (M_((earth)) )/(r^2) G` , here G is Gravitational Constant, and r is distance from center of earth, all the values will remain same except r which will be radius of earth + altitude at which ISS is in orbit.

r = 6721,000 meters, putting this value in above equation gives g = 8.82158145
`m/s^2`.

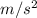(b) We have to essentially calculate centripetal acceleration that equals new 'g'.

`a_(centripetal)=(V^2)/(r) =g` here g is known, r is known and v is unknown.

plugging in r and g in above and solving for unknown gives V = 7699.990192m/s.

(c) S = vT, here T is time period or time required to complete one full revolution.

S = earth's circumfrence , V is calculated in (B) T is unknown.

solving for unknown gives T = 5484.3301s = 1.5234hours.