Question

An accident happens in the lab of Professor Utonium, and a radioactive element X is released in the form of a gas at around 4:00 am. Element X has a short half-life (25 min), and the lab would be considered safe when the concentration of X drops by a factor of 10. Considering the decomposition of element X is of first-order, what is the earliest time Professor Utonium can come back to do experiments in the lab

Answer 1

5:22 am

Step-by-step explanation:

The gas X decays following a first-order reaction.

The half-life (
`t_(1/2)`) is 25 min. We can find the rate constant (k) using the following expression.

`k = (ln2)/(t_(1/2)) =(ln2)/(25min) = 0.028 min^(-1)`

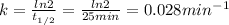
We can find the concentration of X at a certain time (
`[X]`) using the following expression.

`[X] = [X]_0 * e^(-k * t)`

where,

`[X]_0`: initial concentration of X

t: time elapsed

`([X])/([X]_0)= e^(-k * t)\\(1/10[X]_0)/([X]_0)= e^{-0.028min^(-1) * t}\\t=82min`

The earliest time Professor Utonium can come back to do experiments in the lab is:

4:00 + 82 = 5:22 am