Question

Find the Jacobian ∂(x, y, z) ∂(u, v, w) for the indicated change of variables. If x = f(u, v, w), y = g(u, v, w), and z = h(u, v, w), then the Jacobian of x, y, and z with respect to u, v, and w is ∂(x, y, z) ∂(u, v, w) = ∂x ∂u ∂x ∂v ∂x ∂w ∂y ∂u ∂y ∂v ∂y ∂w ∂z ∂u ∂z ∂v ∂z ∂w . x = 1 6 (u + v), y = 1 6 (u − v), z = 6uvw

Answer 1

The Jacobian ∂(x, y, z) ∂(u, v, w) for the indicated change of variables

= -3072uv

Explanation:

Step :-(i)

Given x = 1 6 (u + v) …(i)

Differentiating equation (i) partially with respective to 'u'

`(∂x)/(∂u) = 16(1)+16(0)=16`

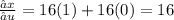
Differentiating equation (i) partially with respective to 'v'

`(∂x)/(∂v) = 16(0)+16(1)=16`

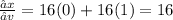
Differentiating equation (i) partially with respective to 'w'

`(∂x)/(∂w) = 0`

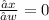
Given y = 1 6 (u − v) …(ii)

Differentiating equation (ii) partially with respective to 'u'

`(∂y)/(∂u) = 16(1) - 16(0)=16`

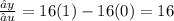
Differentiating equation (ii) partially with respective to 'v'

`(∂y)/(∂v) = 16(0) - 16(1)= - 16`

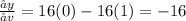
Differentiating equation (ii) partially with respective to 'w'

`(∂y)/(∂w) = 0`

Given z = 6uvw ..(iii)

Differentiating equation (iii) partially with respective to 'u'

`(∂z)/(∂u) = 6vw`

Differentiating equation (iii) partially with respective to 'v'

`(∂z)/(∂v) =6 u (1)w=6uw`

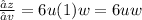
Differentiating equation (iii) partially with respective to 'w'

`(∂z)/(∂w) =6 uv(1)=6uv`

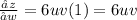
Step :-(ii)

The Jacobian ∂(x, y, z)/ ∂(u, v, w) =

`\left|\begin{array}{ccc}16&16&0\\16&-16&0\\6vw&6uw&6uv\end{array}\right|`

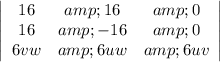
Determinant 16(-16×6uv-0)-16(16×6uv)+0(0) = - 1536uv-1536uv

= -3072uv

Final answer:-

The Jacobian ∂(x, y, z)/ ∂(u, v, w) = -3072uv