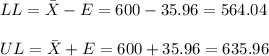Question

A department store wants to know what fraction of its customers in a certain market have store credit cards, and what their average balance might be. Of the 120 customers surveyed, 30 had store credit cards. Amongst those customers, the average balance was $600, with a sample standard deviation of $80. Find the 98% confidence interval for the average credit card balance. ( , ) Round your answers to two decimal places.

Answer 1

The 98% confidence interval for the average credit card balance is

(564.04, 635.96).

Explanation:

We have to calculate the 98% confidence interval on the average credit card balance.

The sample will consist of the n=30 customers that have credit card.

The sample has a mean of $600 and a standard deviation of $80.

As the population standard deviation is estimated from the sample standard deviation, we will use a t statistic.

The degrees of freedom are:

`df=n-1=30-1=29`

The critical value for a 98% CI and 29 degrees of freedom is t=2.463 (this can be looked up in a t-table).

Then, the margin of error is:

`E=t\cdot s/√(n)=2.463*80/√(30)=197.04/5.48=35.96`

Then, the upper and lower bounds of the confidence interval are:

`LL=\bar X-E=600-35.96=564.04\\\\UL=\bar X+E=600+35.96=635.96`