Answer:
Explanation:
GIVEN: Suppose you want to make a cylindrical pen for your cat to play in (with open top) and you want the volume to be
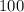 cubic feet. Suppose the material for the side costs
cubic feet. Suppose the material for the side costs
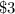 per square foot, and the material for the bottom costs
per square foot, and the material for the bottom costs
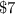 per square foot.
per square foot.
TO FIND: What are the dimensions of the pen that minimize the cost of building it.
SOLUTION:
Let height and radius of pen be

Volume
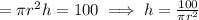
total cost of building cylindrical pen
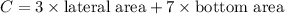
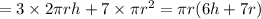
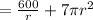
for minimizing cost , putting

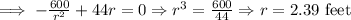
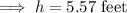
Hence the radius and height of cylindrical pen are
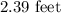 and
and
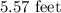 respectively.
respectively.