Question

A standard deck of cards has 52 cards divided into 4 suits, each of which has 13 cards. Two of the suits ($\heartsuit$ and $\diamondsuit$, called 'hearts' and 'diamonds') are red, the other two ($\spadesuit$ and $\clubsuit$, called 'spades' and 'clubs') are black. The cards in the deck are placed in random order (usually by a process called 'shuffling'). In how many ways can we pick two different cards

Answer 1

The number of ways to select 2 cards from 52 cards without replacement is 1326.

The number of ways to select 2 cards from 52 cards in case the order is important is 2652.

Explanation:

Combinations is a mathematical procedure to compute the number of ways in which k items can be selected from n different items without replacement and irrespective of the order.

`{n\choose k}=(n!)/(k!(n-k)!)`

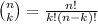
Permutation is a mathematical procedure to determine the number of arrangements of k items from n different items respective of the order of arrangement.

`^(n)P_(k)=(n!)/((n-k)!)`

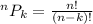
In this case we need to select two different cards from a pack of 52 cards.

• Two cards are selected without replacement:

Compute the number of ways to select 2 cards from 52 cards without replacement as follows:

`{n\choose k}=(n!)/(k!(n-k)!)`

`{52\choose 2}=(52!)/(2!(52-2)!)`

`=(52* 51* 50!)/(2!*50!)\\=1326`

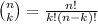
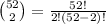
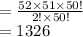
Thus, the number of ways to select 2 cards from 52 cards without replacement is 1326.

• Two cards are selected and the order matters.

Compute the number of ways to select 2 cards from 52 cards in case the order is important as follows:

`^(n)P_(k)=(n!)/((n-k)!)`

`^(52)P_(2)=(52!)/((52-2)!)`

`=(52* 51* 52!)/(50!)`

`=52* 51\\=2652`

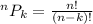
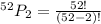
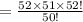
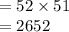
Thus, the number of ways to select 2 cards from 52 cards in case the order is important is 2652.