To solve the problem, it is necessary to apply the concepts related to Faraday's law, for which the voltage induced on a body is defined as follows,
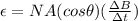
Here,
N = Number of loops
A = Area
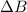 = Magnetic Field
= Magnetic Field
 = Time
= Time
 = Angle between the magnetic field and the surface
= Angle between the magnetic field and the surface
Replacing,
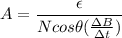
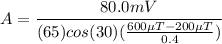
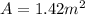
Each side of the coil has a length of
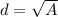
Then the total length of the wire,
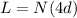
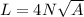
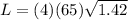
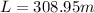
Therefore the total length of the wire is 308.95m