Question

A farmer has produced 1000 apples and wants to sell them. He can sell the apples at two different markets: • At market 1, if the farmer sells x apples, he can sell them for 2 √ x dollars each. • At market 2, if the farmer sells y apples, he can sell them for 4 √y dollars each. Find how the farmer should split his 1000 apples between both markets in order to maximize his revenue.

Answer 1

The farmer should split 800 for market 1 and 200 for the market 2.

Explanation:

The farmer has a total of 1000 apples. He will divide in x apples for the market 1 and y=1000-x for the market 2.

Then, the revenue for the apple sales is the sum of the revenues from market 1 and market 2:

`R=xP_1+yP_2\\\\R=x*2√(x)+(1000-x)4*√(1000-x)\\\\R=2x√(x)+4(1000-x)√(1000-x)\\\\R=2x^(3/2)+4(1000-x)^(3/2)`

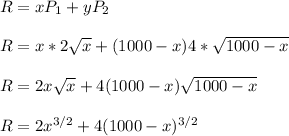
To maximize the revenue, we derive and equal to zero.

`(dR)/(dx)=(d)/(dx)[2x^(3/2)+4(1000-x)^(3/2)]\\\\\\(dR)/(dx)=2*(3/2)x^(1/2)+4*(3/2)(-1)(1000-x)^(-1/2)=0\\\\\\3x^(1/2)-6(1000-x)^(1/2)=0\\\\\\x^(1/2)=2(1000-x)^(1/2)\\\\x=2^2(1000-x)=4(1000-x)\\\\x=4000-4x\\\\5x=4000\\\\x=4000/5\\\\x=800`

Then, the quantity y is:

`y=1000-x=1000-800=200`