Answer:
The mean tuition and fees for private institutions in California is greater than $35,000.
Explanation:
The question is:
The mean annual tuition and fees in the 2013 - 2014 academic year for a sample of 25 private colleges in California was $38,000 with a standard deviation of $7100. A dot plot shows that it is reasonable to assume that the population is approximately normal. Can you conclude that the mean tuition and fees for private institutions in California is greater than $35,000? Use α = 0.05 level of significance an P-value method with the table.
In this case we need to perform a single mean t-test.
The t-test is used since the population standard deviation is not known.
The hypothesis is:
H₀: The mean annual tuition and fees for private institutions in California is not greater than $35,000, i.e. μ ≤ 35000.
Hₐ: The mean annual tuition and fees for private institutions in California is greater than $35,000, i.e. μ > 35000.
The information provided is:
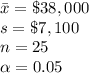
Compute the test statistic value as follows:
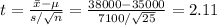
The test statistic value is 2.11.
Decision rule:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.
Compute the degrees of freedom as follows:
df = n - 1
= 25 - 1
= 24
Compute the p-value of t as follows:
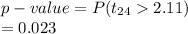
*Use a t-table for the probability.
The p-value is 0.023.
p-value = 0.023 < α = 0.05
The null will be rejected at 5% level of significance.
Thus, concluding that the mean tuition and fees for private institutions in California is greater than $35,000.