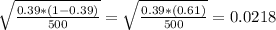Question

According to a study done by the Pew Research Center, 39% of adult Americans believe that marriage is now obsolete. (a) Suppose a random sample of 500 adult Americans is asked whether marriage is obsolete. Describe the sampling distribution of p ˆ , the proportion of adult Americans who believe marriage is obsolete, by answering the following questions: (i) Verify the model requirements. i.e. verify that np(1 – p

Answer 1

The proportion follows normal distribution,

Mean u = 0.39

standard deviation σ = 0.0218

Explanation:

Solution:-

- Lets assume the population proportion ( p ) to be the percentage of adult Americans who believe that marriage is now obsolete.

- We will check for normality:

Lets take, p^ = p (Mean proportion of the distribution)

- The condition of normality,

n*p*( 1 - p ) ≥ 10

Where, n : The sample size taken.

500*0.39*( 1 - 0.39 ) = 500*0.39*( 0.61 )

118.95 ≥ 10

- Hence, with the testing statistics the condition for normality are validated. Hence, the distribution for proportion of adult americans who believe that marriage is now obsolete follows a normal distribution.

- The parameters of the distribution are:

Mean : u = p^ = p = 0.39

Standard deviation σ =
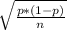`\sqrt{(p*(1-p))/(n) }` =
`\sqrt{(0.39*(1-0.39))/(500) } = \sqrt{(0.39*(0.61))/(500) } =0.0218`