Given:
Given that the length of the rectangle is 5x + 2.
The width of the rectangle is x - 4.
We need to determine the area of the rectangle in a simplified polynomial expression.
Area of a rectangle:
The area of the rectangle can be determined using the formula,
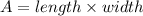
Substituting length = 5x + 2 and width = x - 4, we get;
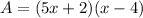
Multiplying the terms, we have;
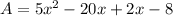
Adding the like terms, we get;
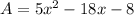
Thus, the area of the rectangle is
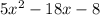
Hence, Option c is the correct answer.