Answer:
a)
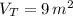 , b)
, b)
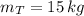 , c)
, c)

Step-by-step explanation:
a) The equation of state for ideal gas is:
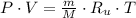
Given the existence of an isothermal process, the following relation is derived:
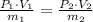
The volume of the other tank is:
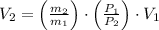

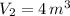
The total volume is:
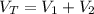
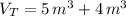
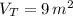
b) The total mass is:
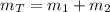
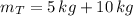
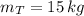
c) The pressure of the gas in the two tanks is:


