Answer:
The function which represents the volume of the box
V(x)=4x³-24x²+36x
where V(x) is in cubic inches.
Explanation:
Cuboid:
- Cuboid is a three dimension shape.
- It has 6 faces and 8 vertices.
- The length of diagonals is
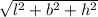 . l= length, b= width and h= height.
. l= length, b= width and h= height. - The total surface area is = 2(lb+bh+lh)
- Volume is = length ×width× height
Given that,
The dimensions of the cardboard is 6 inches by 6 inches.
The length of the side of the squares that removed from each corners of the cardboard is represented by x.
Then, the length of the box is = (6-2x) inches.
The width of the box is = (6-2x) inches
The height of the box is = x inches.
The volume of the box is= length ×width× height
=(6-2x)(6-2x) x cubic inches
={6(6-2x)-2x(6-2x)}x cubic inches
={36-12x-12x+4x²}x cubic inches
={36-24x+4x²}x cubic inches
=(36x-24x²+4x³) cubic inches
=(4x³-24x²+36x) cubic inches
The function which represents the volume of the box
V(x)=4x³-24x²+36x
where V(x) is in cubic inches.