Question

"Which statement best describes ? –6 is in the domain of f(x) but not in the range of f(x). –6 is not in the domain of f(x) but is in the range of f(x). –6 is in the domain of f(x) and in the range of f(x). –6 is neither in the domain of f(x) nor in the range of f(x)."

Answer 1

-6 is not in the domain of f(x) but in the range of f(x)

Explanation:

I think your question is missed of key information, allow me to add in and hope it will fit the original one. Please have a look at the attached photo.

My answer:

The given function is:

f(x) = -2
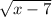`√(x-7)` + 1

To make f(x) is defined, the value inside the square root must be ≥0

<=> x - 7 ≥0

<=> x ≥7

=> -6 is not in the domain of f(x)

How about in the range of f(x)? We can test it by using this ex:

f(x) = -2
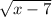`√(x-7)` + 1 = -6

<=> -2
`√(x-7)` = -7

<=>
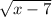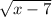`√(x-7)` = 7/2

<=> x - 7 = 49/4

<=> x = 77/4 ≥7

So -6 is in the domain of f(x)

–6 is not in the domain of f(x) but is in the range of f(x)