Question

A parallel plate capacitor is connected to a DC battery supplying a constant DC voltage V0= 600V via a resistor R=1845MΩ. The battery has been connected for a long time. Each plate has an area A=58.3 m2 . The left plate is at ground potential and the right plate is at positive potential. The separation between the capacitor plates is D= 0.3m and all the points in the picture are far from the edges of the plates. The capacitor is placed on board of a space station where there is no gravity present.

In the coordinate system shown in the picture (x is a "horizontal" axis, y is "vertical" although names are purely conventional since there's no gravity), where all lengths are in meters, a positive charge q=3e-05C and mass m=0.4g has been placed directly in point C(0.25,12) and let go. What is the speed, v, of that charge when it reaches point A(0.05,12)?
How long would it take the charge to reach point A?

You decided to repeat the experiment but this time you place the same charge in point C first, and then connect the same power supply to the capacitor via the same resistor to charge it. Do not overcomplicated things: assume that the effect of any magnetic fields is negligible. Assuming that the axes scale on all graphs are the same what is the graph that best represents the horizontal speed of your charge as function of time in this experiment?

To verify your qualitative reasoning, calculate the speed of your charge in your second experiment after the same interval of time it took your charge to move from point C to point A in the first experiment. This is quite a challenging question so don't get disappointed if your group can't get the correct answer. You will not loose any points if you miss this question\

Answer 1

See explanation

Step-by-step explanation:

Given:-

- The DC power supply, Vo = 600 V

- The resistor, R = 1845 MΩ

- The plate area, A = 58.3 cm^2

- Left plate , ground, V = 0

- The right plate, positive potential.

- The distance between the two plates, D = 0.3 m

- The mass of the charge, m = 0.4 g

- The charge, q = 3*10^-5 C

- The point C = ( 0.25 , 12 )

- The point A = ( 0.05 , 12 )

Find:-

What is the speed, v, of that charge when it reaches point A(0.05,12)?

How long would it take the charge to reach point A?

Solution:-

- The Electric field strength ( E ) between the capacitor plates, can be evaluated by the potential difference ( Vo ) of the Dc power supply.

E = Vo / D

E = 600 / 0.3

E = 2,000 V / m

- The electrostatic force (Fe) experienced by the charge placed at point C, can be evaluated:

Fe = E*q

Fe = (2,000 V / m) * ( 3*10^-5 C)

Fe = 0.06 N

- Assuming the gravitational forces ( Weight of the particle ) to be insignificant. The motion of the particle is only in "x" direction under the influence of Electric force (Fe). Apply Newton's equation of motion:

Fnet = m*a

Where, a : The acceleration of the object/particle.

- The only unbalanced force acting on the particle is (Fe):

Fe = m*a

a = Fe / m

a = 0.06 / 0.0004

a = 150 m/s^2

- The particle has a constant acceleration ( a = 150 m/s^2 ). Now the distance between (s) between two points is:

s = C - A

s = ( 0.25 , 12 ) - ( 0.05 , 12 )

s = 0.2 m

- The particle was placed at point C; hence, velocity vi = 0 m/s. Then the velocity at point A would be vf. The particle accelerates under the influence of electric field. Using third equation of motion, evaluate (vf) at point A:

vf^2 = vi^2 + 2*a*s

vf^2 = 0 + 2*0.2*150

vf = √60

vf = 7.746 m/s

- Now, use the first equation of motion to determine the time taken (t) by particle to reach point A:

vf - vi = a*t

t = ( 7.746 - 0 ) / 150

t = 0.0516 s

- The charge placed at point C, the Dc power supply is connected across the capacitor plates. The capacitor starts to charge at a certain rate with respect to time (t). The charge (Q) at time t is given by:

`Q = c*Vo*[ 1 - e^(^-^t^/^R^C^)]`

- Where, The constant c : The capacitance of the capacitor.

- The Electric field strength (E) across the plates; hence, the electrostatic force ( Fe ) is also a function of time:

`E = (Vo*[ 1 - e^(^-^t^/^R^C^)])/(D) \\\\Fe = (Vo*[ 1 - e^(^-^t^/^R^C^)])/(D)*q\\\\`

- Again, apply the Newton's second law of motion and determine the acceleration (a):

Fe = m*a

a = Fe / m

`a = (Vo*q*[ 1 - e^(^-^t^/^R^C^)])/(m*D)`

- Where the acceleration is rate of change of velocity "dv/dt":

`(dv)/(dt) = (Vo*q)/(m*D) - (Vo*q*[ e^(^-^t^/^R^C^)])/(m*D)\\\\B = (600*3*10^-^5)/(0.0004*0.3) = 150, \\\\(dv)/(dt) = 150*( 1 - [ e^(^-^t^/^R^C^)])\\\\`

- Where the capacitance (c) for a parallel plate capacitor can be determined from the following equation:

`c = (A*eo)/(d)`

Where, eo = 8.854 * 10^-12 .... permittivity of free space.

`K = (1)/(RC) = (D)/(R*A*eo) = (0.3)/(1845*58.3*8.854*10^-^1^2*1000) = 315\\\\`

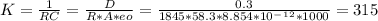
- The differential equation turns out ot be:

`(dv)/(dt) = 150*( 1 - [ e^(^-^K^t^)]) = 150*( 1 - [ e^(^-^3^1^5^t^)]) \\\\`

- Separate the variables the integrate over the interval :

t : ( 0 , t )

v : ( 0 , vf )

Therefore,

`\int\limits^v_0 {dv} \, = \int\limits^t_0 {150*( 1 - [ e^(^-^3^1^5^t^)])} .dt \\\\\\vf = 150*( t + (e^(^-^3^1^5^t^))/(315) )^t_0\\\\vf = 150*( t + (e^(^-^3^1^5^t^) - 1)/(315) )`

- The final velocity at point A for the particle is given by the expression derived above. So for t = 0.0516 s, The final velocity would be:

`vf = 150*( 0.0516 + (e^(^-^3^1^5^*^0^.^0^5^1^6^) - 1)/(315) )\\\\vf = 7.264 m/s`

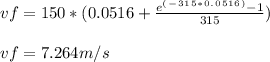
- The final velocity of particle while charging the capacitor would be:

vf = 7.264 m/s ... slightly less for the fully charged capacitor