Question

We survey a random sample of American River College students and ask if they drink coffee on a regular basis. The 90% confidence interval for the proportion of all American River College students who drink coffee on a regular basis is (0.262, 0.438). What will be true about the 95% confidence interval for these data? Group of answer choices The 95% confidence interval is narrower than the 90% confidence interval. The 95% confidence interval is wider than the 90% confidence interval. The two intervals will have the same width. It is impossible to say which interval will be wider.

Answer 1

Correct option:

The 95% confidence interval is wider than the 90% confidence interval.

Explanation:

The (1 - α)% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)* \sqrt{(\hat p(1-\hat p))/(n)}`

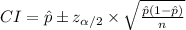
The width of this interval is:

`W=UL-LL\\=2* z_(\alpha/2)* \sqrt{(\hat p(1-\hat p))/(n)}`

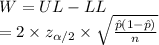
The width of the interval is directly proportional to the critical value.

The critical value of a distribution is based on the confidence level.

Higher the confidence level, higher will be critical value.

The z-critical value for 95% and 90% confidence levels are:

`90\%: z_(\alpha /2)=z_(0.05)=1.645\\95\%: z_(\alpha /2)=z_(0.025)=1.96`

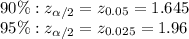
*Use a z-table.

The critical value of z for 95% confidence level is higher than that of 90% confidence level.

So the width of the 95% confidence interval will be more than the 90% confidence interval.

Thus, the correct option is:

"The 95% confidence interval is wider than the 90% confidence interval."