Question

Alex will work on a consulting project for SALT Solutions for 5 days. During these 5 days, the probability that Alex applies for sick leave on a particular day is the same, which is less than 0.5. The probability that Alex applies for his first sick leave on the second day is 0.21. The event that Alex applies for sick leave on a particular day is independent of the event that Alex applies for sick leave on other days. What is the probability that Alex applies for his first sick leave on the fifth day

Answer 1

Probability that Alex applies for his first sick leave on the fifth day is 0.0818.

Explanation:

We are given that probability that Alex applies for his first sick leave on the second day is 0.21.

The event that Alex applies for sick leave on a particular day is independent of the event that Alex applies for sick leave on other days.

The above situation can be represented through geometric distribution because Geometric distribution probability gives us the probability of 1st success in trial.

Since, here we want our first success in the fifth trial, i.e. Alex applies for his first sick leave on the fifth day.

The probability distribution for geometric distribution is given by;

`P(X =x) = p * (1-p)^(x-1) ; x = 1,2,3,4,......`

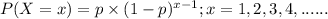
where, p = probability of success which in our question is Alex applies for his first sick leave = 0.21

x = no. of trials = 5

Let X = Day on which Alex applies for first sick leave

So, X ~ Geo( p = 0.30)

Now, probability that Alex applies for his first sick leave on the fifth day is given by = P(X = 5)

P(X = 5) =
`0.21 * (1-0.21)^(5-1)`

=
`0.21 * 0.79^(4)`

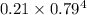
= 0.0818