Question

The highest waterfall in the world is the Salto Angel in Venezuela. Its longest single falls has a height of 807 m. If water at the top of the falls is at 14.2°C, what is the maximum temperature of the water at the bottom of the falls? Assume all the kinetic energy of the water as it reaches the bottom goes into raising its temperature.

Answer 1

Maximum temperature of the water at the bottom of the fall, θ₂ = 16.09°C

Step-by-step explanation:

The height of the waterfall, H = 807 m

At the top of the fall,
`\theta_(1) = 14.2^(0) C`

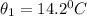
For water, the specific heat capacity, C = 4200 J/kg/°C

Potential energy at the top of the waterfall, PE = mgH

According to the principle of conservation of energy,

Kinetic energy at the bottom of the waterfall = Potential energy at the top

Therefore, KE = mgh

Applying the conservation of energy again,

KE at the bottom = Heat Energy due to raise in temperature

Heat energy due to raise in temperature = MCΔθ

MCΔθ = MgH

CΔθ = gH

Δθ = gH/C

Δθ = (9.81*807)/4200

Δθ = 1.89°C

`\triangle \theta = \theta_(2) - \theta_(1)`

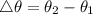
1.89 = θ₂ - 14.2

θ₂ = 14.2 + 1.89

θ₂ = 16.09°C