Question

The 1.18-kg uniform slender bar rotates freely about a horizontal axis through O. The system is released from rest when it is in the horizontal position θ = 0 where the spring is unstretched. If the bar is observed to momentarily stop in the position θ = 46°, determine the spring constant k. For your computed value of k, what is magnitude of the angular velocity of the bar when θ = 30°.

Answer 1

k = 11,564 N / m, w = 6.06 rad / s

Step-by-step explanation:

In this exercise we have a horizontal bar and a vertical spring not stretched, the bar is released, which due to the force of gravity begins to descend, in the position of Tea = 46º it is in equilibrium;

let's apply the equilibrium condition at this point

Axis y

W_{y} - Fr = 0

Fr = k y

let's use trigonometry for the weight, we assume that the angle is measured with respect to the horizontal

sin 46 =
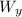`W_(y)` / W

W_{y} = W sin 46

we substitute

mg sin 46 = k y

k = mg / y sin 46

If the length of the bar is L

sin 46 = y / L

y = L sin46

we substitute

k = mg / L sin 46 sin 46

k = mg / L

for an explicit calculation the length of the bar must be known, for example L = 1 m

k = 1.18 9.8 / 1

k = 11,564 N / m

With this value we look for the angular velocity for the point tea = 30º

let's use the conservation of mechanical energy

starting point, higher

Em₀ = U = mgy

end point. Point at 30º

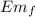`Em_(f)` = K -Ke = ½ I w² - ½ k y²

em₀ = Em_{f}

mgy = ½ I w² - ½ k y²

w = √ (mgy + ½ ky²) 2 / I

the height by 30º

sin 30 = y / L

y = L sin 30

y = 0.5 m

the moment of inertia of a bar that rotates at one end is

I = ⅓ mL 2

I = ½ 1.18 12

I = 0.3933 kg m²

let's calculate

w = Ra (1.18 9.8 0.5 + ½ 11,564 0.5 2) 2 / 0.3933)

w = 6.06 rad / s