Question

Find the average rate of change from x=4 to x=10 for the equation y=2x-3

Answer 1

The average rate of change is 2

Answer 2

2

Explanation:

The average rate of change of the equation during the interval 4 ≤ x ≤ 10

can be represented in this expression if f(x) is substituted for y:

`(f(10)-f(4))/(10-4)`

`=(17-5)/(6)`

`=(12)/(6)`

`=2`

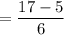
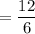
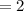
So, the average rate of change (AOC) is 2.

You also could just figure this out by looking at the slope. Since this is a linear equation, the AOC over any interval will always be the same as the slope, since the slope is constant.