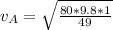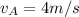Complete Question
The diagram for this question is shown on the first uploaded image
Answer:
The minimum velocity of A is
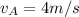
Step-by-step explanation:
From the question we are told that
The length of the string is
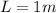
The initial speed of block A is
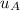
The final speed of block A is
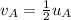
The initial speed of block B is
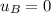
The mass of block A is
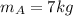 gh
gh
The mass of block B is

According to the principle of conservation of momentum
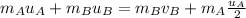
Since block B at initial is at rest
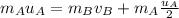
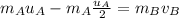
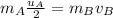
making
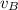 the subject of the formula
the subject of the formula
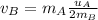
Substituting values
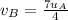
This
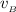 is the velocity at bottom of the vertical circle just at the collision with mass A
is the velocity at bottom of the vertical circle just at the collision with mass A
Assuming that block B is swing through the vertical circle(shown on the second uploaded image ) with an angular velocity of
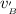 at the top of the vertical circle
at the top of the vertical circle
The angular centripetal acceleration would be mathematically represented

Note that this acceleration would be toward the center of the circle
Now the forces acting at the top of the circle can be represented mathematically as

Where T is the tension on the string
According to the law of energy conservation
The energy at bottom of the vertical circle = The energy at the top of
the vertical circle
This can be mathematically represented as
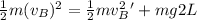
From above
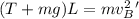
Substitute this into above equation
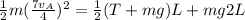
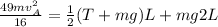
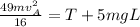
The value of velocity of block A needed to cause B be to swing through a complete vertical circle is would be minimum when tension on the string due to the weight of B is zero
This is mathematically represented as
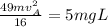
making
 the subject
the subject

substituting values